
Introduction
In Part I, the original GAN paper was presented. Part II gave an overview of DCGAN, which greatly improved the performance and stability of GANs. In this final part, the contributions of InfoGAN will be explored, which apply concepts from Information Theory to transform some of the noise terms into latent codes that have systematic, predictable effects on the outcome.
Motivation
As seen in the examples of Part II, one can do interesting and impressive things when doing arithmetic on the noise vector of the Generator. In the example below from the DCGAN paper, the input noise vectors of men with glasses are manipulated to give vectors that result in women with sunglasses once fed into the Generator. This shows that there are structures in the noise vectors that have meaningful and consistent effects on the Generator output.

However, there’s no systematic way to find these structures. The process is very manual: 1) generate a bunch of images, 2) find images that have the characteristic you want, 3) average together their noise vectors and hope that it captures the structure of interest.
The only “knob to turn” to change the Generator output is the noise input. And since it’s noise, there’s no intuition about how to modify it to get a desired effect. The question is: “what if you wanted an image of a man with glasses — how do you change the noise?” This is a problem because your representation is entangled. InfoGAN tries to solve this problem and provide a disentangled representation.
The idea is to provide a latent code, which has meaningful and consistent effects on the output. For instance, let’s say you’re working with the MNIST hand-written digit dataset. You know there are 10 digits, so it would be nice if you could use this structure by assigning part of the input to a 10-state discrete variable. The hope is that if you keep the code the same and randomly change the noise, you get variations of the same digit.

InfoGAN
The way InfoGAN approaches this problem is by splitting the Generator input into two parts: the traditional noise vector and a new “latent code” vector. The codes are then made meaningful by maximizing the Mutual Information between the code and the Generator output.
Theory
This framework is implemented by merely adding a regularization term (red box) to the the original GAN’s objective function.
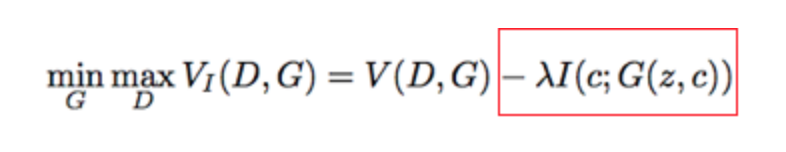
\( \lambda \) is the regularization constant and is typically just set to one. The \( I(c;G(z,c)) \) term is the mutual information between the latent code \( c \) and the Generator output \( G(z,c) \).
It’s not practical to calculate the mutual information explicitly, so a lower bound is approximated using standard variational arguments. This consists of introducing an “auxiliary” distribution \( Q(c|x) \), which is modeled by a parameterized neural network, and is meant to approximate the real \( P(c|x) \). \( P(c|x) \) represents the likelihood of code \( c \) given the generated input \( x \). They then use a re-parameterization trick to make it such that you can merely sample from a user-specified prior (i.e. uniform distribution) instead of the unknown posterior.
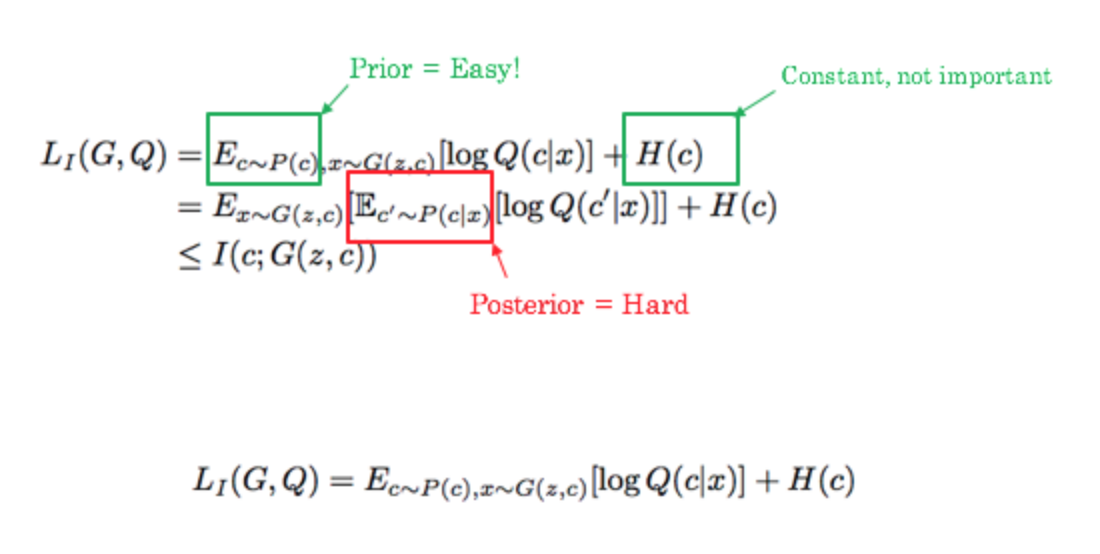
The regularizer term above translates to the following process: Sample a value for the latent code \( c \) from a prior of your choice; Sample a value for the noise \( z \) from a prior of your choice; Generate \( x = G(c,z) \); Calculate \( Q(c|x=G(c,z)) \).
The final form of the objective function is then given by this lower-bound approximation to the Mutual Information:
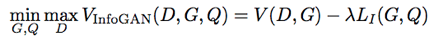
Architecture
As mentioned above, there’s now a second input to the Generator: the latent code. The auxiliary distribution \(Q(c|x) \) introduced in the theory section is modeled by another neural network, which really is just a fully connected layer tacked onto the last representation layer of the Discriminator. The \(Q\) network is essentially trying to predict what the code is (see nuance below). This is only used when feeding in fake input, since that’s the only time the code is known.
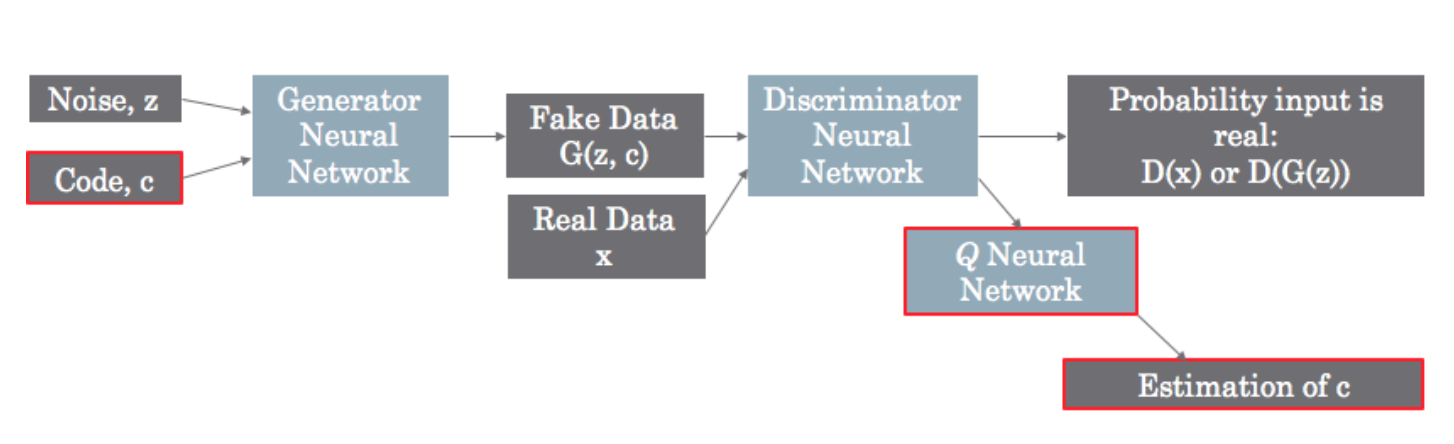
There’s one nuance here that can be difficult to understand. To calculate the regularization term, you don’t need an estimation of the code itself, but rather you need to estimate the likelihood of seeing that code for the given generated input. Therefore, the output of \(Q\) is not the code value itself, but instead the statistics of the distribution you chose to model the code. Once you know the sufficient statistics of the probability distribution, you can calculate the likelihood.
For instance, if you have used a continuous valued code (i.e. between \(-1\) and \(+1\)), you might model \( Q(c|x) \) as a Normal/Gaussian distribution. In that case, \(Q\) would output two values for this part of the code: the mean and standard deviation. Once you know the mean and standard deviation you can calculate the likelihood \( Q(c|x) \), which is what you need for the regularization term.
Results
Initial results were reported by training on the MNIST hand-written digit dataset. The authors specified a 10-state discrete code (hoping it would map to the hand-written digit value), as well as two continuous codes between \(-1\) to \(+1\). For comparison, they trained a regular GAN with the same structure but did not use the regularization term that maximizes the mutual information.
The images below show a process where a particular noise vector is held constant (each row), but the latent code is changed (each column). In part a you see the discrete code consistently changing the digit. Part b shows the regular GAN having essentially no meaningful or consistent change.
Parts c and d show the continuous codes being changed for InfoGAN. This clearly affects things like the tilt and width of the digit. Interestingly, they actually change from \(-2\) to \(+2\) even though training only used values from \(-1\) to \(+1\), which shows that these codes meaningfully extrapolate.

Here are some results on face images. Please see the paper for additional results and explanation.
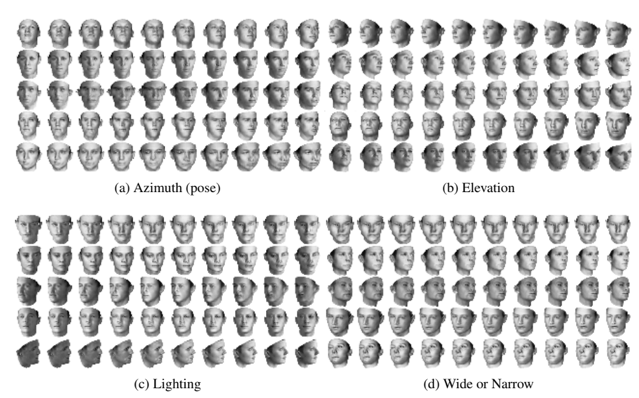

Conclusion
It’s worth stressing that it was never specified in advance that tilt or digit thickness would be useful to separate as codes. The InfoGAN training procedure discovered these attributes by itself — i.e. in an unsupervised fashion. The only thing the researcher does is specify the structure of the latent code.
We’ve seen that by simply adding a term that maximizes Mutual Information between part of the Generator input and its output, the learning process disentangles meaningful attributes in the data and allocates them to this imposed latent code structure.
You Do It
I found the original repo difficult to run since its dependencies are very old. I’ve updated the code so that you can run with modern Tensorflow APIs (version 1.3.0).
Keep Digging
In this 3 part series we’ve covered a few of the major contributions and seen GANs do amazing things. Even still, this barely scratches the surface. There are multiple github repos with a large and growing list of research papers. Here’s one, and here’s another. This is an exciting area of research that’s only growing in maturity and effectiveness. If you find a particular paper you’d like reviewed here, feel free to reach out to me.